Network layer control plane
어떤 역할을하는지
실제 인터넷에서 사용되는 실제구현 체제에대해
- introduction
- routing protocols
- link state
- distance vector
- intra-ISP routing: OSPF
- routing among ISPs: BGP
Introduction
네트워크 계층에 중요한 기능 2가지는 포워딩과 라우팅이다.
포워딩은 한 라우터의 인풋에들어왔을 때 적절한 아웃풋으로 패킷을 전달해주는 역할
이 포워딩을 하는게 데이터 플레인
라우팅은 소스 데스티네이션가지 어떤 페킷을 전달하려고 하는데 어떤 경로를통해서 패킷을 전달할지
이런 경로를 결정하는 것이 라우팅
그리고 이라우팅은 컨트롤 플레인에서 한다.
네트워크 컨트롤 플레인을 구성하는 2가지 방법이 있다.
1. per-router control (traditional)
라우터별로 라우팅 알고리즘을 구현
라우터들끼리 정보교환을 하면서 전체적인 포워딩 테이블을 업데이트해 나아간다.
2. logically centralized control (software defined networking)
SDN이라고도 한다.
이같은 경우는 각각의 라우터별로 동작하는 것이 아닌
전체적인관점에서 컨트롤하는, 리모트 컨트롤러가 상위에 존재한다.
이 리모트 컨트롤러가 라우터 위에서 라우터 정보들을다 모아서 전체적인 정보를 가지고 판단한다.
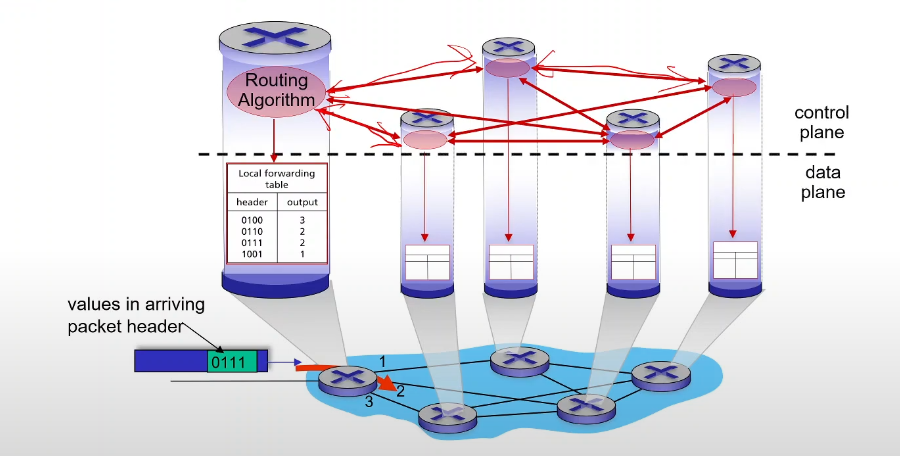
Per-router control plane
라우터 별로 라우팅 알고리즘이 있는 방식
모든 라우터에 라우팅 알고리즘이 동작하게 되고
이 라우터들끼리 서로 통신을 통해서 정보를 교환함으로써 자신의 포워딩 테이블을 업데이트 해 나아간다.
Software-Defined Networking (SDN) control plane
SDN 컨트롤 플레인 같은 경우에는 각 라우터에서 라우팅 알고리즘 처리하는 게아니라
원격의 컨트롤러 역할을 하는 애가 존재한다.
그래서 얘같은 경우는 많은 서버들로 구성되어 있을 수도 있다.
각각의 라우터에서 정보를 모아서 리모트 컨트롤러에 전달해주고
모아진 정보를 토대로 리모트 컨트롤러가 최적의 포워딩 테이블을 업데이트해준다
SND 같은 경우 전체적인 관점에서 경로 결정을 할 수 있어서 좀 더 효과적으로 최적의 경로를 결정할 수 있다.
routing protocols
라우팅 프로토콜에는 어떠한 것들이 있는지 살펴보자
크게는
- link state protocol
- distance vector protocol
두가지가 있다.
간단히 라우팅 프로토콜이 어떤건지 보자.
라우팅 프로토콜의 목적은, 소스에서 데스티네이션까지 이르는 좋은 경로를 찾는 것이다.
좋은 경로에서 경로가 의미하는 것은
라우터들의 순서쌍으로 표시되는 것이다.
좋은 경로에서 좋다라는 의미는
여러 측면에서 좋을 수 있는데,
가장 큰 것은 - 코스트가 낮은 것
코스트도 추상적인데, 이는 속도가 빠르면, 코스트가 낮음을 의미하기도하고,
가장 혼잡이 덜 발생한다고 생각할 수도 있다.
결국 어떤 것에 집중하냐에 따라서 조금씩 다를 순있다.
라우팅은 사실 굉장히 어려운 것이다.
SDN 같은경우 전체적인 관점에서 판단할 수 있다고 했지만, 이러한 일을 하는 것이 쉽진 않다.
전세계의 무수하게 많은 라우터의 모든 경로를 하나의 리모트 컨트롤러에서 컨트롤 할수도 없다.
그래서 결국에는 작은 규모의 네트워크가 아니라면, SDN 방식으로 처리하는 것은 불가능하다고 생각하면 된다.
불안전한 정보라고 할 수있다. 각 라우터별로갖고 있는최소한의 정보만을 활용해서 내 주변의 라우터들이랑만 소통해가며, 최적의 라우팅, 좋은 경로를 찾을 수 있다는 것은 굉장히 어려운 일이다.
라우팅 문제를 일반적으로 나타낼 때는 그래프를 사용한다.
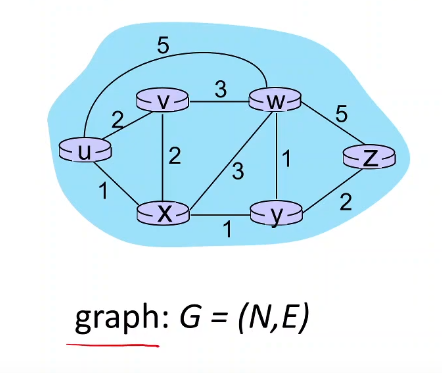
N: node와 E:edge 로 구성된 것을 그래프라고 한다.
각 노드가 의미하는 것은 라우터이다.
그림에서는 6개의 라우터가 존재하는 것이다.
각각의 엣지는 링크를 의미한다.
각 라우터들은 링크로 연결되어 있기 때문에
엣지라는 것은 두개의 노드가 만나서 생기는 부분
그래서 순서쌍으로 표기될 수 있다.
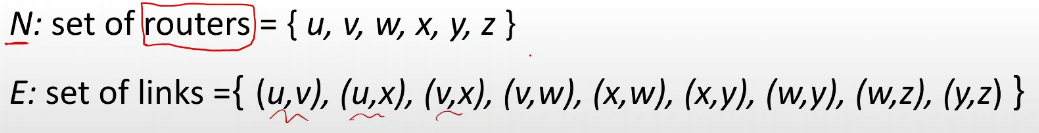
위 그림을 N과 E로 표시할 수 있다.
이를 코스트로 표현할 수 있다.
Ca,b로
예를들어 Cu,v 라고하면 2
그리고 Cu,z라고하면 한번에 갈수 있는 경로가 없으므로 무한대이다.
무한대는 직접 도달할 수 없는 상황임을 나타낸다.
코스트라는 것은 어떻게 결정이 되는 것일까
이같은 경우에는 기본적으로 네트워크 운영자가 설정할 수있다.
밴드위스에 반비례를 하게 할 수도 있을 것이고
모드 1로 설정할 수도 있을 것이다.
그리고 컨제스쳔, 혼잡정도에 따라서 반비례하도록 결정할 수도 있을 것이다.
다양한 방식으로 코스트를 결정할 수 있다.
이와 같이 그래프를 통해서 링크 코스트를 나타낼 수있다.
라우팅 알고리즘을 여러가지방식으로 분류할 수있는데
크게는 글로벌한 관점에서 전체적인 정보를 가지고 판단을 하는 라우팅 알고리즘이냐
분산되서 처리하는 분산 라우팅 알고리즘이냐
이정도로 분류가 되고,
얼마나 자주, 얼마나 빠르게 라우팅 방식이 변하는지에 따라서 분류할 수도 있다.
글로벌이냐 분산이냐 이 부분을 보면
글로벌 방식은 네트워크 전체에대한 완전한 정보를 가지고 최소비용 경로를 계산을하는 것을 의미한다.
이거 자체가 네트워크 전체 링크 비용을알아야하기 때문에 링크스테이트 알고리즘이라고 불린다.
SDN이 이 글로벌 방식을 사용한다.
그에 반해서분산라우팅(전통적인 방식) 알고리즘 방식에서는 모든 정보를 다 가지고 판단을하는 것이 아니다
각각의 라우터들을 최소한의 정보들로 시작한다. 처음에는 자기의 이웃에 있는 라우터의 링크 코스트만을알고 있는 상태에서 시작한다.
그것을 내 옆에 있는 이웃들과 정보를 계속 교환해가면서 조금씩 라우팅 포워딩 테이블을 업데이트해나아간다.
그래서 결국 전통적인 방식 per-router 방식에서는 이런 분산 형태를 사용한다라고 이해하면 된다.
그리고 얼마나 빠르게 라우팅이 변할 수 있는지는 STATIC, DYNAMIC으로 분류할 수 있다.
스태틱 같은 경우 시간이 지남에 따라 자주 변하지 않고 천천히 변하는 방식이고, 다이나믹 같은경우는 굉장히 빠르게 주기적으로 루틴이 업데이트가 된 라우팅 관련 정보들이 업데이트 되고 링크 코스트가 나간다던가 할 때 바로바로 변할 수 있는 라우팅 알고리즘이다.
가장 중요한 건 글로벌과 분산에서 어떤 차이가 있는지이다.
Routing protocols
Link state
라우팅 프로토콜 중에 링크 스테이트 라우팅 알고리즘이 있다.
이중에 가장유명한 것이 다익스트라 알고리즘이다.
Dijkstra's link-state routing algorithm
다익스트라 같은 경우 글로벌한 관점에서 판단하는 알고리즘이라고 생각하면 된다.
중앙에서 모든 네트워크 정보를 다 가지고 판단한다.
각 라우터들 사이의 링크들의 코스트를 전부 알고있는 상태에서 판단을 내린다.
코스트는 어떻게 알수있나 -> 브로드캐스트, 모든 노드한테 내 상태를 뿌리면 된다.
모든 노드들이 결국 같은 전체적인 정보를 가지고 판단을 내리기 때문에 최적의 결과를 얻을 수 있다.
다익스트라 알고리즘을 통해서 하나의 노드에서 다른 노드에 이르는 비용을 최소로하는 경로를 찾을 수 있게 된다.
이 경로를 계산해낼 수 있다고 한다면
최선의 순서쌍으로 표현해 낼 수 있다.
경로가 개선이 되면서 포워딩 테이블을 업데이트하면된다.
그래서 비용을최소로 하는 비용을최소로할 수 만있다면 포워딩 테이블을 업데이트할 수 있다.
한 라우터에서 어떤 라우터로의 최소 비용 경로를 알기 위해서는 노드 개수만큼의 이터레이션을 돌아야한다.
어떤게 최적의 최소 비용 경로인지 계산할 수 있다.
Cx,y: x에서 y에 이르는 직접 연결된 링크의 코스트
D(v): 한 라우터 기준으로 봤을 때 목적지 v까지 으르는, 현재까지 계산된 그 경로의 최소비용
P(v): 현재 라우터에서 부터 어떤 목적지 v까지 이르는데, v까지 이르기 바로 전의 노드가 어떤건지 의미
N': 완벽하게 최소 경로가 결정된 애들을 모아놓은 집합


위와 같은그래프가 주어져 있다고 가정하자.
이 정보는 모든 라우터가 이 정보를 모두 가지고 있다.
현재 라우터는 u라고 가정하자
u라는 라우터에서 시작하는데, 여기서 시작하면 내가 나에게 이르는 경로는 당연히 0이다.
이미 최소경로를 알고 있다고 가정하고, N'에 u를 집어넣고 시작한다.
그리고 각각의 부위에 이르는 경로 vwxyz에 으르는 경로를 테이블로 만든다.
u에서 시작해 v까지 가려고 할 때 최소 경로는 2이므로, D(v)=2 이다. 그리고 P(v)=u 가 된다.
w를 보면 직접 경로가 있고 코스트가 5이다. 그래서 D(w)=5, P(w)=u 이다.
x -> D(x)=1 P(x)=u
y는 직접 경로가 없으므로 무한대이고, z같은 경우도 무한대이다.
그래서 0번째 스탭을 정리하자면
| step | N' | D(v),P(v) | D(w),P(w) | D(x),P(x) | D(y),P(y) | D(z),P(z) |
| 0 | u | 2,u | 5,u | 1,u | ∞ | ∞ |
이 다음에 최소값을 찾는데 N'에 아직 추가되지 않는 애를 찾는다.
이중에서 가장 작은게 D(x) =1 이다.
그래서 x를 N'에다가 추가시켜준다.
그러면 N'은 ux가 되고 u,ux 로 가는 경로 중 코스트가 가장 적은 것을 고르면 된다.
D(v)를 보면

u로 가는 경로의 코스트는 2이고, uxv로 가는 코스트는 3이므로,
더작은 u로 가는 경로를 택한다.
D(v)=2,P(v)=u가 된다.
w도 보면, 원래는 바로가면 5였는데, u->x = 1, x->w = 3 이므로 D(w)=4로 업데이트가 되고, P(w)=x로 업데이트 된다.
x같은 경우는 이미 x에 도달했으니까 여기는 값을 계산할 필요 없고
y같은 경우에는 u->x = 1 x->y=1 이므로 D(y)=2이고, P(y)=x 가 된다.
u, ux에서 z로 바로 갈 수 있는 방법이 없으므로 이는 무한대∞가 된다.
그래서 1 스탭을 정리하자면
| step | N' | D(v),P(v) | D(w),P(w) | D(x),P(x) | D(y),P(y) | D(z),P(z) |
| 0 | u | 2,u | 5,u | 1,u | ∞ | ∞ |
| 1 | ux | 2,u | 4,x | 2,x | ∞ |
아까처럼 반복을 해보면, 여기서 가장 작은 것이라고 하면 v,y가 있다 이 둘중에 하나를 고르면 되는데,
일단 y를 골라보자
N'에 y가 추가가 되고, 이를 다시 계산하면 것을 반복하면 된다.

uxy에서 v는 u->v인 2가 가장 최솟값이므로 D(v)=2, P(v)=u 이다.
w는 u->x=1, x->y=1, y->w=1 이므로 D(w)=3, P(w)=y로 업데이트 된다.
x와 y는 이미 도달해 있으니까 넘거가고,
z는 u->x=1, x->y=1, y->z=2 로 D(z)=4, P(z)=y로 업데이트 된다.
2번째 스탭을 정리하자면,
| step | N' | D(v),P(v) | D(w),P(w) | D(x),P(x) | D(y),P(y) | D(z),P(z) |
| 0 | u | 2,u | 5,u | 1,u | ∞ | ∞ |
| 1 | ux | 2,u | 4,x | 2,x | ∞ | |
| 2 | uxy | 2,u | 3,y | 4,y |
그리고 이중에서 최소코스트를찾으면 v이므로 N'에 v를 추가해주고
v,x,y는 도달했으니 넘어가고 나머지 w,z를 보자
w는 u->x=1, x->y=1, y->w=1 D(w)=3, P(w)=y 로 같고,
z또한 같이 D(z)=4, P(z)=y로 같다.
3스텝을 정리하면
| step | N' | D(v),P(v) | D(w),P(w) | D(x),P(x) | D(y),P(y) | D(z),P(z) |
| 0 | u | 2,u | 5,u | 1,u | ∞ | ∞ |
| 1 | ux | 2,u | 4,x | 2,x | ∞ | |
| 2 | uxy | 2,u | 3,y | 4,y | ||
| 3 | uxyv | 3,y | 4,y |
여기서 최소 코스트는 w이므로 N'에 w를 추가해주고
x,y,v,w는 도달했으니 넘어가고, z만 보자
z는 변경없이 기존 있던 값이 가장 최솟값이므로, D(z)=4, P(z)=y
4번째 스탭을 정리하면
| step | N' | D(v),P(v) | D(w),P(w) | D(x),P(x) | D(y),P(y) | D(z),P(z) |
| 0 | u | 2,u | 5,u | 1,u | ∞ | ∞ |
| 1 | ux | 2,u | 4,x | 2,x | ∞ | |
| 2 | uxy | 2,u | 3,y | 4,y | ||
| 3 | uxyv | 3,y | 4,y | |||
| 4 | 4,y |
마지막으로 z까지 모든 u에서부터 시작해서 모든다른 라우터에 이르는 최소경로를 결정했다.
그럼 여기에 맞춰서 포워딩 테이블을 업데이트할 수 있다.
그럼 u의 포워딩 테이블은
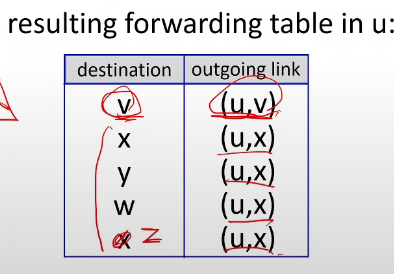
위와 같이 각라우터별로 최적의 경로를 포워딩 테이블에 업데이트하게 된다.
그런데 만약에 u에서 z로가는최소 경로를 알고 싶다면,
z에서 거꾸로 가며 P(?)를 찾으면 된다.
P(z)=y고, p(y)=x, P(x)=u
이렇게 해서 u->x->y->z 이렇게 된다.
아까처럼 동점이 있다면 아무거나 고르면 된다.
이 다익스트라 알고리즘의 복잡도를 보면 n개의 라우터가 존재한다고 가정하고,
결국에 하나의 라우터를 기준으로 봤을 때 각각의 다른 라우터로 가는 경로들을 계산을 했었다. 결국의 n번에 반복을 해야한다.
처음에는 n개의 라우터가 있다면 n개를 모두 비교해봐야한다.
그리고 그 다음엔 n-1개,
...
마지막에는 1개만 남는다.
결국에 1부터 n 까지의 합이므로
n(n+1)/2 가 되고,
계산을 하면 차수가 n^2이므로,
복잡도는 n^2가 된다.
그런데 이걸 구현할 때 최소힙이라고 하는 것을 활용하면 n^2을 nlogn으로 만들 수도 있다.
그리고 메시지 복잡도 측면에서도 봤을 때
각각의 라우터가 자기의 링크 정보들을 다른 라우터들한테 브로드캐스트를 해줘야 한다.
그래서 이 경웨 가까운 라우터 마다 n개의 다른라우터들한테 보내야 하니까 애도 n^2이 된다.
이 알고리즘은 코스트를 계산을 할 때 링크 코스트를 컨체스쳔, 트래픽으로도 계산 가능하다고햇는데, 링크 코스트를 네트워크에서 발생하는 트래픽에 기반해서 결정할 때 route oscillation, 라우팅을 알고리즘을 하는데, 왔다갔다 할 수 있다는 문제가 있다.
라우터 동기화 시점을 각각다르게해서 해결할 수 있으며,
혹은
디스턴스 벡터라는 것을 활용하면 이런 문제를 방지할 수 있다.
'개발👩💻 > 네트워크' 카테고리의 다른 글
| 13-1:Network Layer: control plane (0) | 2021.06.03 |
|---|---|
| 12-2:Network Layer: control plane (0) | 2021.06.03 |
| 11-2:Network Layer: Generalized Forwarding (0) | 2021.05.28 |
| 11-1:Network Layer: IP: the internet protocol (0) | 2021.05.28 |
| 10-1:Network Layer: Data Plane (0) | 2021.05.27 |



